There's no way you'll understand how the Benham’s disk produces the colors if you don’t have a true explanation of how the light produces the colors in general. Since the explanation of the contemporary science is an utter nonsense, therefore every explanation of the Benham’s disk is an utter nonsense, too.
Hence, to answer this question, I will first give you a true explanation of how the light makes the colors appear.
For the colors to appear, the light must experience on its way of propagation a resistance of a more or less transparent matter. The most impressive example is an opalite stone:

This is a real photograph of a longish opalite stone (it’s two centimeters long in reality) illuminated with white LED lamp from the right.
When you look at this stone in a half dark room, you see no colors at all. You see approximately this image:
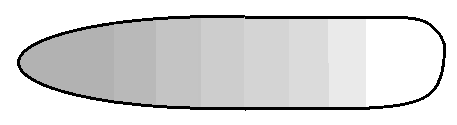
The opalite is a kind of glass. With no additives in it, it is colorless and transparent just like the ordinary glass. But when additives in the form of fine powder are added, then colors appear in it. The last drawing shows how the powder is distributed in the stone from the photograph. On the right there are very little additives. As we go to the left, the concentration increases.
Let me jump for a moment to something else. When a body moves through space filled with air, then higher pressure is created in front of it, while lower pressure behind it. The higher pressure is Plus, the lower pressure is Minus. I use to call it the ‘principle of the arrow’ (− >—> +).
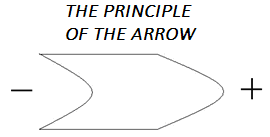
The greater the velocity of the body is, the stronger is the Plus in front of it as well as the Minus behind it.
This principle can also be found in the so-called Bernoulli’s principle (please see THE GREATEST HOAX IN THE HISTORY OF SCIENCE! and AN EXPLANATION OF SOME EXTRAORDINARY EXPERIMENTS WITH PRISMATIC COLORS!
Moreover, the same principle is also present in the light when it encounters resistance of a more or less transparent matter on its way of propagation. The front of the light turns yellow-red which is the result of a higher light-pressure, while the rear of the light turns violet-cyan which is the result of a lower light-pressure.
Look at these beams obtained by means of a diffraction grating. The arrow in the image is added by me (source Wikimedia):

Regarding this image, I claim that these colors wouldn’t have appeared if there is no air surrounding the diffraction grating. In other words, the air is also an inevitable actor in this performance. If the grating is placed in an absolute vacuum, then no colors will emerge. The white light will remain white after passing through it. An absolute vacuum is hard to achieve. But it would be a sufficient proof if the colors get paler in conditions close to an absolute vacuum.
Look also at this drawing:
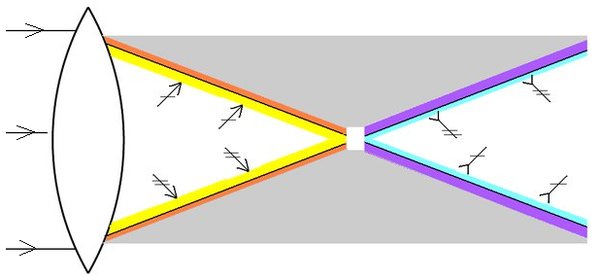
This is what is happening when white light passes through a chromatic convex lens. Before the focal point there is a friction between the light-front and the air, therefore higher yellow-red light-pressure here (marked with arrows without tails). After the focal point there is friction between the light-rear and the air, hence lower violet-cyan light-pressure (marked with arrows without heads).
That is the truth about the convex lens. The image you can see in the textbooks when the so-called chromatic aberration is discussed is a shameless lie of the contemporary physics.
Let me ask you something regarding the things I just said. How come the colors suddenly change their frequencies (colors are EM-waves with different frequencies, aren’t they???!!!) in a point far from the refraction surface?! Let me hear your explanation of this experiment!
Now, let’s get back to the Benham’s disk. First, let’s consider this kind of disk:

I call it double plane spiral, because there are two spirals that interwine. If we place it on a spinning top and then spin it clockwise, we see only circles which move outward like waves when we drop a stone in still water (figure a below). However, when we spin it counter-clockwise, then we see circles which move toward inside (figure b below).
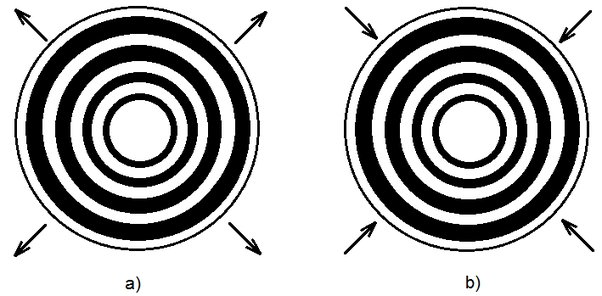
If we look carefully at the disc during its spinning clockwise, we see reddish circles appear along the outer edges of the white circles as long as the disk is spinning fast, and as the spinning is slowing down, the circles turn into yellow (the experiment should be carried out near a window through which daylight comes in, but not directly from the sun). Along the inner edges of the white circles appear cyan circles as long as the spiral is turning fast, and as the speed decreases, the circles turn into blue-violet (in the figure (a) below is shown what is happening when the disk is turning slower).
But look, the same is happening when the disk is spinning counter-clockwise, only it is now reversed. The reddish and the yellow circles appear along the inner edges of the white circles, while the cyan and the blue-violet circles appear along the outer edges of the white circles (figure (b) below).
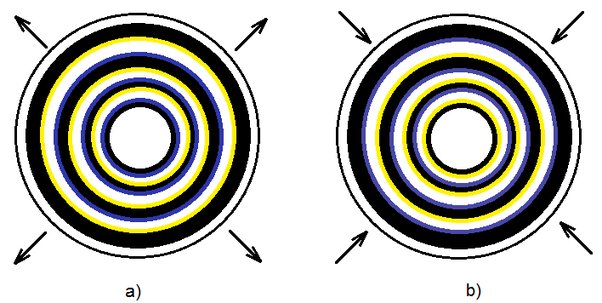
We see that here recurs the same principle as in the previous phenomena: the yellow and the red color appear at the front, while the blue-violet and the cyan at the rear side. For, when the circles are moving outwards, then the outer edges of the white circles are the front and the inner edges are the rear of the light.
We know that the light is reflected only from white surfaces. Thereby the angle of reflection is equal to the angle of incidence. However, this applies only when the surface is still. If it is moving, then the light gets an additional angle in the direction of motion, thus the angle of reflection becomes greater. [The video game “Pong” also incorporates this reality.] So the light gets an additional friction with the air which is responsible for the reddish color at the front and the cyan color at the rear when the disk is spinning faster, but also for the yellow color at the front and the blue-violet at the rear when the disk is spinning slower.
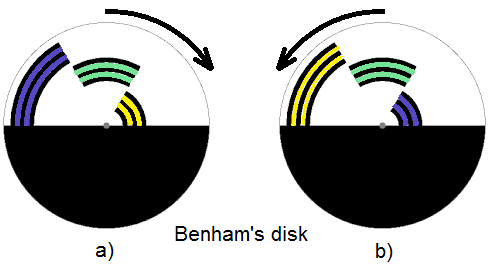
Finally, this is the Benham’s disk in its usual form:
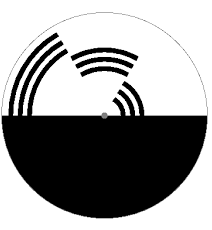
When the disk is spinning clockwise, then we see approximately the colors as shown in the figure (a) below. However, when the disk is spinning counter-clockwise, then we see the colors as shown in the figure (b).
Look please at this segment of the disk:

It is like a fork entering the darkness (i.e. the air without light in it). From the “tines” of this fork the light is reflected with an increased angle of reflection toward the air of the darkness when the disk is turning clockwise.
So, what is my assertion regarding this disk?
There will be no colors if there is no air around the disk. The emergence of colors follows here, as everywhere else, the principle of the arrow.
See also:
WHY IS THE SKY BLUE? HOW DOES LIGHT MAKE COLORS APPEAR?
