This article on how the light produces the colors I begin with phenomena that everyone can see in daily life.
If we look at the flame of a candle or a cigarette lighter in a dimly lit room, the flame is blue-violet in the lower part and yellow-orange in the upper part. If the part of the wick running over the wax is very short, then the flame is very small and it appears only blue.
The flame of a gas stove is also blue, but as soon as we increase the gas supply, yellow tongues appear in the upper part of the flame.
The smoke of a cigarette, whose smoke columns are not very dense, appears blue against a dark background, whereas yellow-orange against a light background (for example a window in daylight).
When the sun rises or sets, the sky around it is yellow-orange or even red. This color is also projected onto the opposite horizon or onto the clouds at various points in the sky, while the upper part of the sky retains its blue color. If we look closely at the sunset horizon, we can sometimes also notice that a greenish part appears between the lower yellow-red and the upper blue part.
During larger volcanic eruptions, when the air currents spread the smoke towards the sun, it was noted that the sky turned orange-red (such a case has been described during an eruption of Krakatau).
The cloudless day sky appears blue. The higher we look the deeper blue it gets, especially on clear days by low air humidity. The lower we look, the brighter the blue of the sky, even turning into whitish. Mountaineers climbing mountains of thousands of meters tell us that the sky’s color is the deeper blue the higher they get.
The mountains very often appear blue, darker blue the nearer, lighter blue the more distant ones.
Dirty windows appear orange-yellow. If we apply a thin layer of sour milk to a clean glass surface and look through it toward a window with daylight, the surface appears yellow-orange. The same surface against a dark background appears faintly blue.
This phenomenon can be observed much more intensively on opalite stones, which can be found in jewelry stores. The opalite is a mineral, a sort of glass with certain additives. When we look through this stone toward a light source, it appears yellow, orange or red, depending on the concentration of additives in it (we need several stones with various concentrations to see this). If there are no additives in the opalite, it is transparent and colorless. At low concentration the stone turns yellow, with the increase it turns orange, to change to red and become almost opaque at very high concentration. The same stone against dark background appears violet at low concentration, blue at greater, to turn to bright blue (i.e. cyan) and then to whitish at very high concentration. If a small white LED lamp is neared the stone in the darkened room, then the yellow (orange or red) color is projected onto the opposite wall, while the stone itself is violet (blue, cyan or white).
If a longish stone with moderate and uniform concentration of additives is illuminated with a white directional LED lamp along its long axis, then it gives the following picture:

If a longish stone with a quick uniform increase of the concentration of additives along the long axis is illuminated with a white directional LED lamp along that axis from the side with the lower concentration, then it gives the following picture:

This is a real photograph of such an opalite stone (illuminated from right):

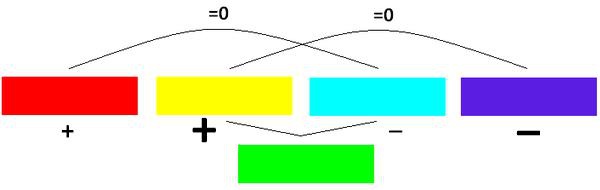
All the aforementioned phenomena and experiments, but also others whose description will follow, come down to a single principle, that of plus and minus. In this particular case we can call it “principle of an arrow”. The front part of the arrow is plus, the rear minus. We call the front part ‘plus’ because it has a penetrating effect, the back part ‘minus’, because it has a suctioning effect (+ <−−−−< −) (the sign '<' appears both at the front and at the back of the arrow, so that already in it there are the plus and the minus (+<−). Please read also: The Bernoulli’s principle can be found in the electric current, too – Electromagnetism – New Theories Forum
In the flame of the candle and that of the lighter we recognize the same arrow pattern. In the front of this ‘fiery arrow’ appears the plus color (yellow), in the back the minus color (blue-violet). As we will see later, the yellow and the violet are the two fundamental plus/minus colors of the world. The red (including the orange) is nothing else but weakening of the yellow; the cyan (including the blue) is nothing other than weakening of the violet. When the strong plus (yellow) meets the weakened minus (cyan), their overlapping bears the green. In this color dominates of course the plus, which can be seen, among other things, on the leaves of the trees. In autumn they turn from green to yellow, then to orange, and even to red on some trees, but never to cyan, blue or violet.
If the strong minus (the violet) overlaps with the weakened plus (the red), this gives birth to magenta. From the mixing of the strong plus (the yellow) and strong minus (the violet) we get nothing, that is, we get their cancellation, which means more or less dark gray.
When we observed the small opalite with moderate concentration of additives against a dark background, it appeared blue. What does it actually mean, to observe the stone against a dark background? It means that we are positioned sideways to the stone considering the direction of the light, seeing the ‘tail’ of the light permeating through it. Therefore the stone appeared with a minus color. Since it is small and with moderate concentration of additives, it cannot hold up the light, that is, the light passes through it and makes a bright yellow spot on the opposite wall (of course, we couldn’t see that by diffused daylight, but we have perceived it with the help of the directional white light of the LED lamp. To see the yellow color by daylight, we hold the stone close to the eye looking through it in the direction where the light comes from). But when the stone was longish with moderate and uniform concentration of additives, then, illuminated along the longitudinal axis, it absorbs i.e. withholds the light to a great degree, thus the yellow and the red color project already in it on its far side. Therefore it gives the image of a candle or a lighter. When the concentration increases rapidly along the longitudinal axis, then the cyan catches up the yellow, thus the green color appears here as well.
From what has been said so far, we can conclude that the colors are born when the light encounters matter as an obstacle on its way of propagation; or, in other words, when it comes to friction between the light and the matter. For the eye which looks toward the light source, the light is white when there is no or little matter between the eye and the source, that is, when there is no or just a little friction. As the concentration of matter increases, so the light becomes yellow, then orange, then red; at the end, at very high concentration, the light is completely attenuated and it turns black. In order to increase the resistance it is not always necessary to increase the concentration of the matter, but the thickness of the material layer (through which the light passes) can be increased as well. When the sun is rising or setting, the thickness of the atmosphere layer is the largest, which is why the light is red. The upper part of the sky (i.e. the atmosphere) is blue because in relation to this part we are positioned sideways and see the rear of the light permeating the atmosphere.
As the sun rises further, so the thickness of the material layer through which we directly see the sunlight diminishes, thus the light becomes orange, then yellow, to finally become to a great degree white, because the thickness of the layer, that is, the resistance is small and insufficient to color the light considerably. However, the rest of the sky is blue for the same reason we have already stated.
When we observe a small opalite stone with low and uniform concentration of additives sideways, it is blue-violet, with greater concentration blue and even greater light blue (i.e. cyan), and then turns into whitish. As the concentration increases, the light can permeate the stone ever less, thus the permeation gradually transitions into reflection of the light from the additives; and the white light, when reflected, remains white. For the same reason the part of the sky in the zenith is blue-violet (the thinnest layer to the dark, immaterial universe, especially at higher altitudes), the lower part is light blue, to end in whitish on the horizon. For the same reason we see often the near mountains blue-violet (especially if they are dark, that is, forested), the farther ones blue, and the very distant whitish. This largely depends on the current degree of the air humidity. The more transparent the air is (i.e. with less vapor), the darker blue the near mountains are (this does not apply, of course, to the very close ones).
Hence, the gradations when we see the plus-side and the minus-side of the light, starting from low concentration of matter and going to higher, or starting from a thin, going to a thicker material layer by unchanging concentration, are the following:
White → yellow → orange → red → black (plus-side)
Black → blue-violet → blue → cyan → white (minus-side)
The images below show a kind of spiral, which we will call a double plane spiral. ‘Double’ because there are two spirals that intertwine. But which spirals are we talking about, the white or the black? The question makes no sense, because the one cannot exist without the other.
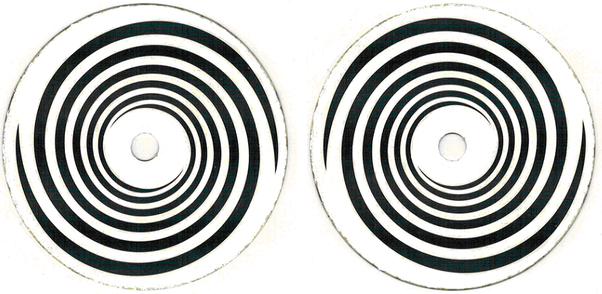
If we place the first spiral on a spinning top and turn it to the left, then it will expand (the circles will move outwards), that is, it will push us (+). If we observe carefully what is happening when the spiral is turning, we will notice that thin red strips appear along the outer edges of the white circles as long as the spiral is spinning fast, and as the spinning slows down, the strips turn into yellow (the experiment should be carried out near a window through which daylight comes in, but not directly from the sun). Along the inner edges of the white circles appear thin light blue strips as long as the spiral is turning fast, and as the speed decreases, the strips turn into blue-violet.
If we turn the spiral to the right, then the circles are moving inwards (−), so that now the red or the yellow strips are visible at the inner edges of the white circles and the light-blue or the blue-violet strips at the outer edges.
Regarding the second spiral (on the right), it happens the same: when the circles are moving outwards, the red and the yellow strips appear on the outer edges of the white circles, and when they are moving inwards, these colors appear on their inner edges.
We see that here recurs the same pattern as in the previous phenomena: the yellow or the red color appear on the front and the blue-violet or the light blue on the rear side. For, when the circles are moving outwards (we say circles because the white and black spirals appear as circles as the top spins), then the outer edges of the white circles are the front and the inner edges are the rear of the light.
Since the light is reflected only by the white circles, we can imagine light and dark tubes, or, let’s say toroids above the spiral. These toroids are static when the spiral stands still, however, they move outwards or inwards when it spins. To clarify what follows, we will make a comparison with a tennis ball bouncing off a horizontal surface at an acute angle. Thereby the angle of reflection is equal to the angle of incidence. However, this applies only when the surface is still. If it moves in the same direction as the projection of the ball’s trajectory onto the surface, then the ball receives an additional movement, thus the angle of reflection is no longer equal to the angle of incidence, but greater. [Do you remember the video game “Pong”?]
Something similar can be assumed with light. When it is reflected by the white circles which move let’s say outwards, the light gets additional movement towards the dark parts, in other words, it penetrates sideways into the matter, i.e., into the air over the dark circles which are in front of it. The sideways penetration means more intense friction than the frontal penetration, so this friction will produce plus colors on the front (that is, on the outer edges of the white circles) and minus colors on the rear side of the light (that is, on the inner edges of the white circles). During faster turning of the disk, the white circles move faster, the reflection angle is greater and therefore the friction intensity too, hence red color on the front and blue on the rear. As the rotation slows down, so the red turns into yellow and the blue into violet due to the diminishing of the reflection angle and therefore the intensity of the friction, too.
It should be kept in mind that we deal here with diffuse light. This is mentioned for the reason that the direct light in some parts of the disk would receive additional motion, but in other parts retardation.
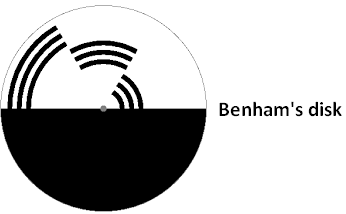
From the aforesaid the reader can conclude on his/her own, how we would explain the appearance of colors on Benham's disk when it is turning.
Let us consider the following simple experiment. We take a sheet of paper and hold it about 15-20 cm in front of one eye (the other eye is closed) opposite to an uncurtained window through which daylight comes in. If we observe the edge of the sheet carefully, we will notice a thin yellow strip along the edge. We can also pierce with a needle a small hole in the sheet and look through it towards the window. Then we will notice yellow circle along the edge of the hole.
If we now move the sheet in front of our eye so that its edge and the dark edge of the window, which of course is farther away, form a narrow gap, then we will notice that a blue strip appears at the farther edge. If this arrangement is fixed and the gap is quite narrow, then green emerges in the middle between the plus- and minus-colors.
Now we go over to experiments with a triangular glass prism (hereinafter: prism). The experiments that will be carried out we can divide into subjective and objective ones. Subjective experiments are called those when we hold the prism in front of our eyes and look through it, and objective ones are called those when we let directed light pass through the prism and then, at a greater or lesser distance behind the prism, the path of the light is blocked with a white wall which may also be a white sheet of paper that we hold behind the prism.
The prisms are usually made equilateral with three equal angles of 60°. One of them, in this case no matter which, is called the (refractive) angle of the prism (also called apex angle). It can be directed upwards (▲) or downwards (▼). In essence, there is no difference between the two possibilities. We will choose the second variant as more practical. Therefore, unless explicitly stated otherwise, the variant of refractive angle being directed downwards is assumed.
If we hold the prism horizontally in front of our eyes and see through it the objects around us, we notice that they take on additional impressive colors. On closer inspection, we perceive that these colors appear where abrupt horizontal or oblique dividing lines (boundaries) between lighter and darker surfaces can be seen, whereas on the monochrome surfaces and on those with gradual transition from light to dark as well as on vertical abrupt ones, it is not the case. In the last variant, however, we will notice additional colors if we hold the prism obliquely or vertically in front of our eyes. The additional colors are paler if the transitions are milder, i.e., when the boundary contrast is weaker, and they are stronger when the transition is abrupt. They are actually the strongest on boundaries where the contrast is maximal, that is, between deep black and bright white.
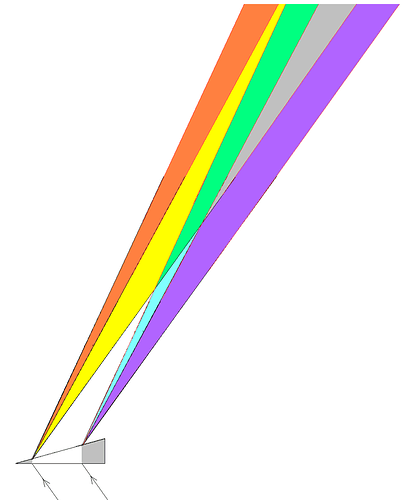
Therefore, we will begin our experiments with detailed observations of boundaries between black and white areas. We can do it by preparing white papers with black areas on them, or vice versa; or we can attach on a window, through which daylight comes in, opaque cardboards into which certain shapes are cut. The attached cardboard represents a black area, and where there is none, it is a white area. If we attach a cardboard in the shape of the image below (left) and the rectangle is wide (it is meant the smaller side), and if we look at this shape through the prism from a few steps away, then we see the image in the middle. А yellow-red strip appears at the upper formerly black-white boundary and a violet-cyan one at the lower boundary. If we turn the prism so that the refractive angle is upwards, then we see exactly the same image, only turned 180°. We notice that in the yellow-red strip the yellow stripe is noticeably wider than the red one, and in the violet-cyan strip the violet stripe is noticeably wider than the cyan one. If we approach the rectangle without losing sight of it through the prism, the yellow-red and the violet-cyan strip become ever narrower, and as we get very close, they practically disappear. If we move away from the rectangle, then the colored strips spread. As they spread, so the yellow and the cyan stripe begin to approach each other, the white space between them is getting narrower, and at the moment when the two colors touch, a green color appears.

As we move farther away, so the cyan disappears, more precisely, it is completely covered by the yellow and converted into green, so now we see four colors: red, yellow, green and violet (the right image above). As we move even farther, a dark field begins to appear between the green and the violet, and even farther, between the red and the green. The gap between the green and the violet can be clearly seen when we observe through the prism a distant, not very bright white street light.
If we think about where we actually see the image through the prism, we realize that it is shifted and that we see it significantly below its true position when the refractive angle is turned downwards, and significantly above its true position when the angle is turned upwards (the eye always projects the image in a straight line; for example, when we see an image in a mirror at an acute angle, then we see it as if it were behind the mirror. Moreover, when we look through a window the image is also shifted, except in the case when we look through it at right angle.). We see the colored rectangle also a bit curved, namely, curved upwards in the first case (▼), and curved downwards in the second (▲) (here again we get a kind of arrow shape with the plus-colors at the front and the minus-colors at the back) . This is because when we look through the prism, we see both in straight and oblique direction at the same time. In the straight direction there is smaller thickness of the prism in front of our eyes, in the oblique direction larger thickness (figure below). With larger thickness of the prism, the image is shifted more.
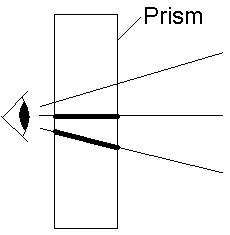
This curvature does not appear in objective experiments when the sunlight falls on the prism, but it can be seen when the light source is a small white LED lamp that we hold close to the prism. The reason is that the sun is a broad and distant source, thus its rays can be regarded as parallel, whereas the LED lamp is a small and near source and therefore to it the same applies as to our eyes.
If we observe the same image through a prism with a smaller refractive angle, say 15°, the only difference is that the image is shifted less and the width of the colored strips is smaller, of course at unchanged distance of the observer from the image. In order to get the same width of the strips with this prism as with the equilateral one, we have to move farther away from the window.
If we look at the image through prisms with equal refractive angles, from the same distance, but made of different types of glass, let's say from flint glass, crown glass and acrylic glass, then here again we will notice differences in the displacement of the image and the width of the colored strips. With the flint-glass prism the image is mostly shifted and the thickest strips can be seen, because the flint-glass has the largest refractive index of these three types of glass, that is, the light is mostly refracted by it.
Now on the window we attach two square cardboards, horizontally placed, one above, the other below, which touch each other only with their vertices (left image below). When we look at this image through the prism we will see the image on the right. We have brought the yellow-red and violet-cyan strips on the same line. We notice that there is equality in width of both groups as wholes, but also separately: the width of the yellow stripe is the same as that of the violet, and the width of the red stripe is the same as that of the cyan. What is also very important here is that the red stripe appears at the expense of the black field, while the yellow one at the expense of the white field. In other words, a part of the black field has turned into red and a part of the white field has turned into yellow. Consequently, on the other side a part of the black field has turned into violet, and a part of the white field into cyan. Where previously was the boundary between the white and the black, now that line is the border between the yellow and the red, i.e. between the violet and the cyan.

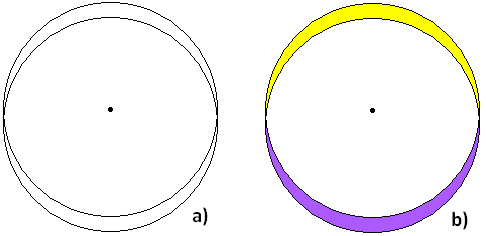
Let's move on to observing a circle. For that purpose we cut a circle in a cardboard and attach it to the window (left image below). When we look at it through the prism we see the image on the right. The circle has taken on an elliptical shape with the well-known yellow-red belt above, and the violet-cyan one below. They are widest at the top and the bottom edge and become narrower to the left and the right side, to completely disappear at the extreme left and right points. If we fix a small circular cardboard in the center of the circle, in other words, if we place a central point in it, and although this small circle observed through the prism becomes colored and therefore not clearly visible, we can still notice that it appears in the upper part of the ellipse.
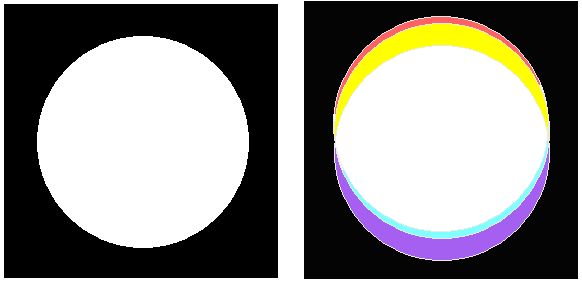
Instead of observing white rectangles and circles on a black background, we can do the opposite - observe black rectangles and circles on a white background. For this purpose, we attach on the window an opaque cardboard, once in a shape of rectangle, another time in a shape of circle. We will get the images below. In this case, if we cut the rectangle or the circle smaller or if we move away from the window, then the violet and red color will approach each other and at the moment of their overlapping, a magenta color is born. In the first case the wider yellow(+) and the narrower cyan(–) overlap to produce green. This time the wider violet(–) and the narrower red(+) overlap producing magenta.

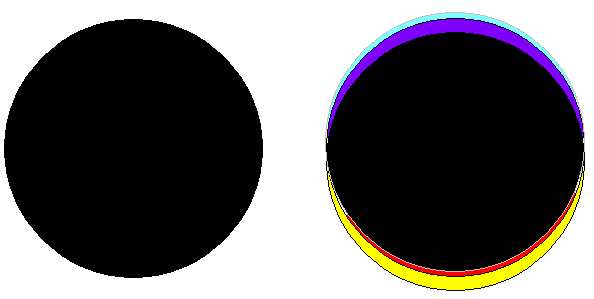
In the case of the black rectangle, it is as if we had two light sources, one up and one down (the rectangle can be imagined very long). The “head” of the lower light with the plus-colors manages to catch up with the “tail” of the upper light with the minus-colors and their overlapping gives birth to magenta.
If on a white sheet of paper we draw horizontal narrow black stripes so that they are of same width to each other, but also to the white space between them (i.e. to the white stripes) and if we look at this image through the prism from a certain distance, then only two colors remain in the image: the green and the magenta. In other words, instead of black and white, we now see magenta and green stripes. In the white stripes the yellow has merged with the cyan becoming green, in the black stripes the violet has merged with the red becoming magenta (white stripe → green; black stripe → magenta).
Instead of fixing cardboards on the window, we can carry these experiments out in such a way that we observe the mentioned shapes as black and white areas on paper. We will see through the prism exactly the same images as before. But in this case we can make the black and white areas in different shades of gray, from black to white. We will notice that absolutely nothing changes in the results, except that the colors get paler the less the contrast is between the darker and the brighter shades of the gray areas. In order to accomplish this grading on the window, we need papers with different transparency. This can be achieved by using tracing paper in different number of layers.
The simplest objective experiment we can make with the prism is the following: in a room in which direct sunlight enters we hold with one hand the prism with the refractive angle downwards, of course in the field of the direct light, and with the other hand behind the prism we hold a white sheet of paper. If we hold the sheet very close to the prism, then we will see only a regular bright rectangle without any colors. As we move the sheet away from the prism backwards and upwards at once, then a violet-cyan strip appears on the upper edge of the rectangle, and a yellow-red strip on the bottom edge. With the further withdrawal of the sheet, the strips widen, the middle white field of the rectangle narrows, and in the moment when the yellow and cyan stripe overlap, green appears. Now we have a continuous colored spectrum.
All that has been described so far for the subjective experiments with the prism fully recurs in the objective experiments; therefore we don’t feel it is necessary to repeat it again. We will only describe the way these experiments are carried out.
On the incident or emerging surface of the prism we stick an opaque paper and once we cut a rectangle, another time a circle in it. Then we hold the prism in the sunlight as we did in the previous experiment. This corresponds to the observing of the rectangle and the circle in the subjective experiments. Moving the sheet of paper behind the prism corresponds to the changing of our distance from the window with the attached cardboards.
Another time on the prism we stick two opaque squares that touch each other with the vertices. In order to get a magenta color we stick only an opaque strip horizontally in the middle of the prism. To carry out the experiments with darker or brighter gray surfaces, we need to stick on the prism more or less transparent papers.
Glass prisms that can be purchased have not large incident surface, so that no significant amount of sunlight can fall on them. By covering it partly with opaque papers we reduce the amount of light further. Therefore, the colored phenomena at a not large distance behind the prism already weaken. Glass prisms with bigger surface would be quite heavy. Johann Wolfgang Goethe for this purpose used a water prism in his experiments. It was a prism-shaped ‘aquarium’ fixed in a wooden construction with the refractive angle directed of course downwards. The prism had a large incident surface so that the phenomena at longer distances didn’t weaken significantly. Its drawback was that after every experimenting the water had to be exhausted because the lime would have blurred the glass.
What we have said earlier, that there is no difference between the subjective and the objective experiments, is not entirely true. There is still one small and baffling difference. When we observed a white field on a black background through the prism (▼) in a subjective experiment the plus-colors were up, the minus-colors down, whereas in an objective experiment the colors are placed reversed.
The colors obtained with the help of the prism are called refractive colors, because the Latin term “refraction” refers to the change of direction of light when it falls at an acute angle on its way from one medium to another which have different densities. The refraction is always inclined to the denser medium, that is, the made “curve” encompasses larger part of the denser medium (figure below).

We can compare the change in the direction of light with a vehicle passing over at considerable speed at an acute angle from solid asphalt into soft muddy ground or vice versa. The vehicle then inevitably changes the direction of movement.
When a vehicle makes a curve as it moves, then the inner wheel travels a shorter distance than the outer. Once the vehicle enters the soft earth, one wheel will collide with the greater resistance of the soft earth earlier than the other, causing the vehicle to turn to the side where the first wheel travels a shorter distance. The same principle applies in the opposite case.
The light undergoes two refractions on the prism, one at the entering and the other at the emerging surface. For the birth of the refractive colors there is no need of a double, but only of a single refraction. For example, when a circular beam of light falls on water surface at an acute angle, then it refracts, and on the bottom of the water, if it is white, the same can be noticed as on the screen in the objective experiment, in which an opaque paper with a circular hole was stuck on the prism surface.
When a beam of light propagates in space, its frontal surface is at right angle to the direction of propagation. We call this frontal propagation of light. But when the beam makes an ‘arc’, that is, when it is refracted, then it propagates sideways, meaning that its frontal surface is no longer perpendicular to the direction of propagation. We call this sideward propagation of light. This mode of propagation entails an increased friction of the light with the matter, and the sharper the ‘arc’ described, the more intense the friction. The friction causes birth of colors, and the plus-colors in the objective experiment are always on the outer side - we would like to say on the outer front of the ‘arc’ - and the minus-colors on the inner front. We see that the same pattern recurs here as in the previous cases: the plus-colors hurry ahead, while the minus colors run after. (The straight lines of the incident and the refracted beam can also be considered as two arms of the arrow sign (<). The plus-colors are on the front, and the minus-colors on the rear of the arrow, but of course only on the refracted arm.) Thereupon it can be assumed that the angle for which the light is slanted, i.e., the angle (β) between the new frontal surface and the normal of the new direction is equal to the angle (α) by which the light is refracted, i.e. that β = α.
It follows that if we mount a prism at one end of a vacuum tube and a white screen at the other end, then from the falling light on this prism no colors on the screen will appear, because although the light is slanted and spreads sideways, it has still nothing to rub against behind the prism.
When we observed through the prism the white circle on black background with a point in the center, we noticed that the point appears in the upper part of the elliptical shape. In the figure below two identical circles are drawn, one slightly below the other, with a central point belonging to the upper circle. This image actually represents the slanting of the light beam after the refraction. Although the circle resembled an ellipse, it is not an ellipse, because two circles one below another cannot form an ellipse. The figure (b) shows where the two basic and - in the case of the prism - wider colors appear, the yellow and the violet. For greater clarity the narrower colors, red and cyan, are not shown. The red appears outside the circles over the yellow, and the cyan inside the circles over the violet.
An important term that we need in order to understand the further details of the refractive colors is the divergence of light, that is, the cone-shaped propagation of a light beam. Every light diverges more or less, even the laser light. For example, if we direct a laser beam from the roof of a tall building onto the street at night, we will notice that the bright circle on the street is considerably larger than that on a nearby surface.
When a light beam refracts, its heretofore uniform divergence to all sides becomes non-uniform, namely more intensive in the direction of refraction and less intensive in the opposite direction (figure below). The greater the refraction, the more intensive the divergence.
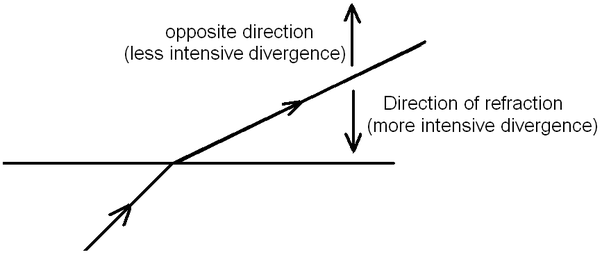
The yellow stripe is wider. In its width manifests itself the larger divergence in the direction of refraction. The red stripe is less wide. In its width manifests itself the smaller divergence in the opposite direction [1]. Since here the light spreads counter the direction of refraction, its attenuation is the greatest, so it appears red in color. The same happens to the other side, where what was said for the yellow applies to the violet, and that for the red applies to the cyan. When the yellow and the cyan meet at a certain distance behind the prism, their overlapping gives birth to green. A little farther the cyan is completely overlapped by the yellow, so now there are only four colors: red, yellow, green and violet. However, the overlapping does not mean that the colors are mixed as chemical colors so that they no longer exist as separate, but they continue to spread out as separate entities, thus a little farther the yellow begins to overlap with the violet. What's going on here? When something moves circularly or spirally, then in one point of the circle it has one direction of motion, but in the diametrically opposite point it moves in the contrary direction. Yellow, overlapping with the violet, encounters something that has a 180° contrary movement; therefore, the two cancel each other out, resulting in the appearance of a more or less dark gray part that comes at the expense of the violet. This happens because both have the same intensity, which was not the case with yellow and the cyan. Although they have contrary motion too, the intensity of the cyan is less than that of the yellow, so the resulting green is actually a slightly stifled yellow. Even farther, the cyan will penetrate into the red field resulting also in cancellation, that is, in a dark part that goes at the expense of the red stripe, for here applies the aforesaid about the intensities.
[1] It is interesting that chemical additives in the glass can change the intensity of divergence. With certain additives that are more on the acid plus-side (e.g. metal oxides) and with certain additives that are more on the alkaline/base minus-side, two different glasses can be obtained which have the same refractive index, i.e. they “bend” the light equally, but the width of their colored strips are different. They are wider in the glass with oxide (+) additives and narrower in the glass with alkaline (–) additives.
The appearance of gray parts between the prismatic colors in combination with something else, which will be left undiscussed for now, is the basis for understanding of what in science is called a discrete spectrum.
All that has been said above applies also in the case when instead of opaque paper with a circular hole we stick on the prism a circle of opaque paper. But this time instead of overlapping of the wide yellow and the narrow cyan, an overlapping of the narrow red and wide violet takes place, resulting in magenta.
The following pairs: yellow-violet, red-cyan and green-magenta are the plus-minus pairs that cancel each other because of their equal intensity. These pairs are also called complementary colors.
If we draw in a computer program a yellow field on a white background and stare at it for a while, then we close the eyes and wait for a few seconds ‘looking’ into the blackness, then we will ‘see’ a violet field with the same shape forming out of the blackness. Instead of closing the eyes, we can point them to a nearby white wall. The same effect happens. If we repeat the experiment while looking at a violet field on the screen, then after closing the eyes we ‘see’ a yellow field. The experiment can be repeated with the other pairs: red-cyan and green-magenta. Trying out with other ‘inter-colors’ we can easily determine which color is complementary to which.
If we stare at the double plane spiral for ten seconds or more while it is spinning and then point our eyes to a nearby surface, we will notice that now we see the opposite of what we were looking at before. If the spiral was contracting (–), then the surface we look at thereafter is expanding (+); and if the spiral was expanding (+), then the surface we look at thereafter is contracting (–).
From the previous two groups of experiments we can conclude that after a certain stimulus the eye does the opposite to relax: if the stimulus was plus, then minus follows for relaxation and vice versa, similar to a rolled up paper which afterwards we roll up in the opposite direction to better flatten it.
We said that in the subjective experiments with prism the plus and minus colors switch their places in comparison to the objective ones. It comes therefrom, that in the objective experiments the outer side of the made ‘arc’ is its front, thus the plus colors appear there, while in the subjective experiments the front is the inner side of the ‘arc’. We can explain this on a single refraction experiment. In the image below the eye is in water, while the light source is in the air above the water. I believe the figure speaks for itself.
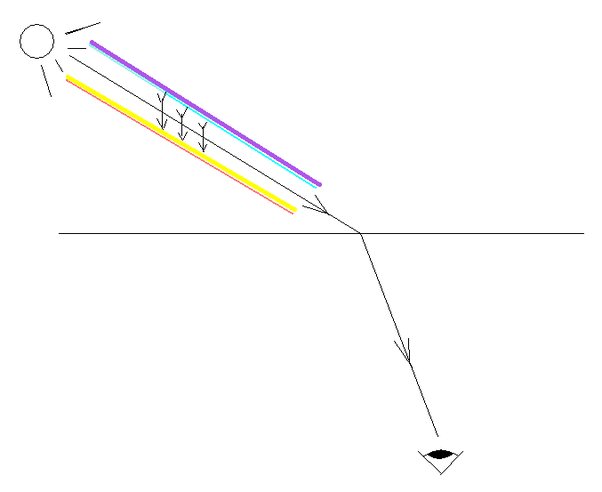
If we place a coin on the bottom of a bucket filled with water and look at it from above, we notice that the coin seems closer than it actually is, that is, closer compared to when the bucket is empty. We can say that the light in the water, as a medium where it is confronted with greater resistance, experiences greater compactness of its spirality than in air. Here we can make an analogy between the light and the electricity. Electricity also experiences a greater compression of its spirality in the wires with greater electrical resistivity (ρ).
If we hold a convex lens (i.e. a magnifying glass) before one eye - the other is closed - and look through it at a distant white circular street light at night, then we see it surrounded by a violet-cyan ring. As we move the lens slowly away from the eye, the light circle along with the ring enlarges so that at one point everything dissolves in whiteness on the whole lens. With the farther moving of the lens, a distinct white circle begins to form again, which is now shrinking. But this time the violet-cyan ring has turned into a yellow-red [footnote 1]. However, not only this can be noticed. Everything that we see now is upside down. If we carry out this experiment as an objective one, by sending through the lens white light and catching the image on a white sheet of paper behind the lens, then we get the opposite situation. When the sheet is close to the lens, the bright circle has a yellow-red ring. With the moving of the sheet farther away, the circle shrinks to a point; thereafter it begins to grow, but this time with a violet-cyan ring. Now the image is turned upside down.
[1] If the lens has a large focal length (which happens when the curvature of the lens is very mild), then the length of our arm will not be enough to see the yellow-red ring. In this case the magnifying glass should be stuck to the window and we should move away from it looking constantly at the light through the lens.
At this point, on the example of this objective experiment, I would like to call on the reader to think dynamically in moving pictures: the sheet moves away from the lens, the image is upright, the colors are plus; the image shrinks to a point, then it turns upside down (what we can call a minus image), the colors also turn into minus.
The experiments with a concave lens do not have the diversity of the previous ones. In a subjective experiment with this lens, we see the street light surrounded by a yellow-red ring and the directed light through the lens in an objective experiment with a violet-cyan ring. There are no inverted images here, therefore no transitions from minus to plus colors or vice versa.
A convex lens can be regarded as a very large number of small prisms arranged in a circle with refractive angles directed outwards. The surfaces of these prisms are not flat, but slightly curved. The same applies to the concave lens, except that here the refractive angles of the prisms are directed inwards, that is, towards the center.
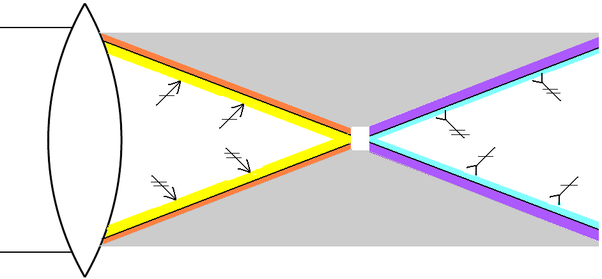
The image below shows the objective experiment with a convex lens. Before the light focuses in a point, its front rubs with matter; after the focal point it occurs with its rear. Hence, yellow-red color in the first section and violet-cyan in the second.
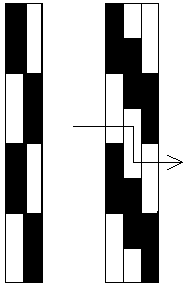
If we cut two equal squares from а polarizing film and put one on top of the other and look through them, then we can see quite well. If we now slowly rotate one of the squares, the picture gradually darkens and when we have rotated it by 90°, that is, when the square exactly covers the other again, the picture is completely dark. In this position the squares become opaque. By rotating it further, the picture brightens, so that in the next 90° position the squares are well transparent again. In few words, with every 90° turn we get alternately full brightening and full darkening, and a gradual transition in between.
Every polarizing film, though transparent, it is still considerably dark. We can notice this well if we lay a piece of crystal clear glass and a piece of polarizing film next to each other. Therefore, we can assume an existence of regularly ‘woven’ dark ‘threads’ throughout the film.
If we print two identical copies of the double plane spiral on tracing paper, then put the one on top of the other and look through them, we will notice that the same happens: at every 90° rotation we get brightening and darkening. This cannot happen with another type of spiral. With a single spiral it happens at every 180° rotation, with a triple spiral at every 60°, with a fourfold at every 45°, etc.
What does the double spiral actually represent? In it we have the same principle that we have already encountered in the EM-element. And in this element there is at the same time the principle of the arrow. (please see A new explanation of the electric current!)

If we cut a third equal square from the polarizing film and place it between the other two (when they are arranged in a state of opacity) either in the 0° or 90° position, then nothing changes, i.e. the opacity remains. But if we begin to slowly rotate the middle square, the picture gradually brightens. When we reach the 45° position with it, the picture is completely brightened and if we continue to rotate it further, the picture darkens again and is completely dark at 90°. The same recurs with the further rotation of the middle square.
When it is in the 45° position, the middle square serves as a bridge between the other two. For the first square we could say that it is at 12 o'clock position, the middle one at 1.30, and the third at 3 o'clock, so the spirality can be established through the three, that is, the light can pass through the foil squares.
The aforesaid can be described also a little differently: the first figure on the left schematically and principally shows the situation with only two polarizer foils when they are in arrangement of opacity. The second figure shows the situation when between the two is inserted the third polarizer foil at an angle of 45° relative to the others. At this arrangement of the foils the light can pass through, which is symbolically shown with the broken arrow. This is possible thanks to the inherent spirality of light.
P.S. The orthodox believers in the theory that light consists of colors often give as an argument for their belief the example of RGB, that is, the mixing of the three colors, red, green and blue-violet to get white. Regarding this I have to say the following:
-
Pure white is an equivalent to light. It reflects the maximum possible light. Pure black is an equivalent to darkness. It reflects no light. Gray is a mixture of white and black and through gradual darkening of the white, that is, through darker and darker shades of gray, the other extreme, that is, the black is reached.
Just as any shade of gray is darker than white and lighter than black, so any color is darker than white and lighter than black, too. To any color we can associate a corresponding gray shade, so that in respect to the amount of reflected light, the two surfaces will be identical. In fact, every color is also a kind of darkening of the white.
Just as it is impossible to get white by mixing two gray shades, so it is impossible to get white by mixing any other two or more colors. -
Every light source in its core is white. In fact, there is no light other than white. If we look at, let’s say, a blue LED lamp, we can notice that in its core it is white. The blue color is an aura around the core. It is so with any other "colored" light.

(first image borrowed from https://mercola.com)
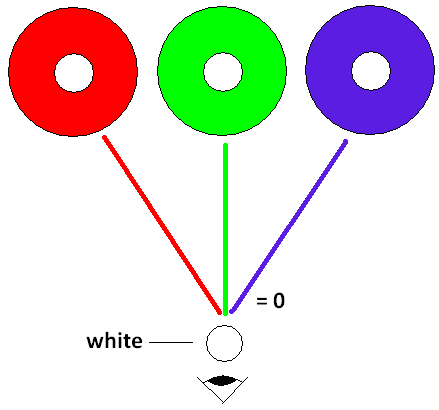
If three "colored" lights - red, green and blue-violet - are placed next to each other, from the mixing of the green and the blue-violet we get cyan, which is complementary color to red, so this leads to their cancellation. What is left is only the white.
We can say this as well: mixing green and red will produce yellow, which is complementary to blue-violet, so this leads to their cancellation and what is left is only white.
Another ridiculous argument for the current theory is the so-called Newton disc. It is a disc painted in colors. When the disc spins, the colors are mixed and it is said that this mixture is white. Yet it is not white, but gray. The darker the colors are, the darker the gray is. The paler the colors are, the lighter the gray is.