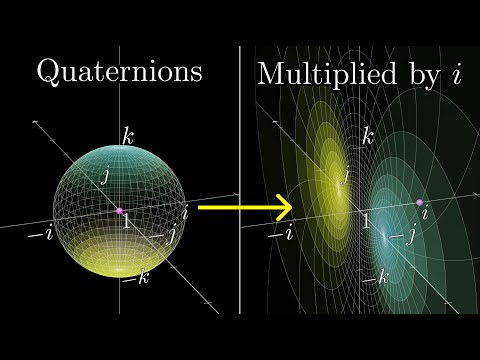
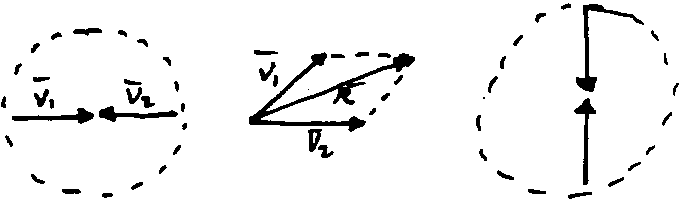List members , Tom Bearden had come up with an excellent explanation of how electrogravitation was forgotten when the mathematical tool of Quaternion was discarded in favour of Vector Mathematics . When Oliver Heaviside truncated Maxwell's original 20 equations to just 4 , he essentially eliminated Scalar force :-
Maxwell's lost unified field theory of electromagnetics and gravitation
T. E. Bearden
It is revealing to discuss the basic genesis of modern electromagnetic theory starting with Maxwell's original theory expressed in quaternions (1) (2) (3).
Most of us are familiar with four fundamental equations of theoretical electromagnetics, universally taught in Western universities and colleges as "Maxwell's Equations". (See Table 1) It may come as somewhat of a surprise, at least to the casual scientist or engineer, that these equations never appeared anywhere in Maxwell's fundamental "Treatise". (4) (5). In fact, they are entirely due to the interpretation of a single brilliant man, Oliver Heaviside (6) (7).
The Early Struggle in EM Theory
Maxwell wrote his first paper on electromagnetics in 1864 - during the time of the US Civil War, and the paper was published in 1865 (8). At that time, the modern form of vector analysis had not yet been completed (9). The prevailing mathematics available for use in deeper electrical physics was the quaternion theory founded by Hamilton in 1843 (10). Hamilton's quaternion theory was the first significant nonarithmetic mathematical system (11).
Maxwell's original expression of his theory was written in quaternions and quaternion-like mathematics. It attracted singularly attention (12), and was considered only speculation until Heinrich Hertz discovered electromagnetic waves in 1885-1888 (13) (14).
Indeed, early on, mathematicians strongly attacked Maxwell for his - to them revolutionary and startling concept that energy could exist in a massless wave and travel through space (15). While that concept is considered self-evident to today's scientist and engineer, it was considered incredible and starting when Maxwell proposed it.
TABLE 1:
DIFFERENTIAL VECTOR FORM OF HEAVISIDE/MAXWELL EQUATIONS
Maxwell's equations (Gaussian units):
![]()
![]()
![]()
![]()
Combining these equations with the Lorentz force equation and Newton's Second Law of Motion is thought to provide a complete description of the classical dynamics of interacting particles, and electromagnetic fields.
Two vectors, not interlocked.
a. Two vectors which are not interlocked by the medium (abstract vector space), simply pass through each other and do not interact. They cannot be said to have a common resultant, except fleetingly.
Two vectors, interlocked.
b. Two vectors which are interlocked by the medium (abstract vector space) do not pass through each other but do interact. They can be said to have a common translation resultant externally. However, internally they must be said to produce a stress in the medium (abstract vector space).
Figure 1: A serious flaw exists in the application of the abstract vector analysis to physical systems. Only when the local gravitational effects are fleeting or negligible, does this flaw become negligible - and the vector theory become a valid representation (model).
Maxwell himself was an excellent mathematician of the time (16) (17), of ability far beyond that of most of the contemporary electrical theorists and experimenters (18) (19). Possibly as a result, both his early lectures and writings were therefore difficult - or even nearly impossible - for his contemporaries to comprehend (20). It required the translation of Maxwell's theory (20) into the abbreviated and clearer, more readily understood vector mathematics of Oliver Heaviside (22), and the publication of clearer and much simpler expositions by Heaviside (23), before "Maxwell's theory" - or at least the Heaviside subset of it - began to capture the attention of leading university electrical scientists (24).
At the same time, the major expositor of the tough, obtuse and very difficult quaternion theory - Prof. Peter Guthrie Tait - was a stubborn, fiery, argumentative mathematician rather than a physicist. He also delayed preparing his exposition of quaternion theory until a number of years had passed and his mentor, Hamilton, had had time to rework his own obtuse, difficult book (25) (26). While Tait delayed, scientists and engineers beset with practical problems in the real world of industry were frantically seeking a simplified theory that: (1) could be readily grasped and understood, and (2) could immediately be applied to solve their practical problems of equipment design and building. The only available and accessible simplified theory of electromagnetism that fitted their urgent needs was the clear, simplified and imminently practical work of Oliver Heaviside - who himself held no degree and was self-educated.
Accordingly, the die was cast. Working engineers and leading scientists focused upon Heaviside's vector interpretation of Maxwell's difficult quaternionic expressions. In Heaviside's version the engineering calculations were enormously eased, and electrical engineers could get solutions to their pressing problems and get on with their business of constructing electrical devices and electrical machinery. Except for a very few mathematical scientists who could handle the heavy labours of quaternions, Heaviside's electromagnetics rapidly became the ipso facto standard.
A major schism developed between the increasingly isolated few quaternionists and the steadily multiplying vectorists, slowly growing to white heat in the literature A final duel to the death became inevitable.
The duel exploded before the turn of the century and a short, sharp debate occurred among about 30 or so scientists and in about 12 journals (27). The culmination was quick - complete victory by the vectorists. The quaternion EM theory was simply cast out, and the scientific community turned to Heaviside's limited vector subset of the Maxwell theory. The short "debate" only confirmed what had already become an accomplished fact: the Heaviside vector analysis translation of the EM subset of Maxwell's theory was already universally accepted and applied.
Vector Analysis Excised Electrogravitation
Ironically, in their great haste to seize upon Heaviside's simpler, clearer explanation of EM and get on with solving practical engineering problems, the nineteenth century scientists gave up something of far greater value: the unification of EM and gravity, and the ability to directly engineer gravitation itself.
Maxwell had actually written a unified field theory of electromagnetics and gravitation - not just the unification of electricity and magnetism as is commonly believed (28). Further, this can readily be shown by examining some significant even startling - elementary differences between quaternion mathematics and the present vector mathematics (29) (30) (31) (32).
Let us briefly look at one of these key differences, to show that the present vector mathematics expression of Maxwell's theory is only a subset of his quaternion theory (33).
What Heaviside's theory specifically omitted was electrogravitation (KG) - the ability to transform electromagnetic force field energy into gravitational potential energy, and vice-versa. And that has been omitted because of the assumptions of the vector theory in the nature of: (1) EM vector field combination, and (2) a zero-vector resultant of the interaction of multiple nonzero EM force vectors (34) (35).
Briefly, in Heaviside's vector mathematics, the abstract vector space in which the vectors exist has no stress nor consequent "curvature" in it. That is, the mathematical vector space does not change due to interactions between the vectors it "contains". This, of course is not necessarily true in the "real space" of the physical world. Thus when such an abstract vector space and its concomitant coordinate system are taken to model physical space (physical reality), the model will be valid only when the physical space itself has no appreciable local curvature, and is in a state of total equilibrium with respect to its interactions with observable charged particles and masses.
So abstract vector theory implicitly assumes "no locked-in stress energy of the vector space itself". By assumption, the only interactions are between the objects (the vectors) placed in/on that space. Therefore, when two or more translation vectors sum or multiply locally to a zero-vector translation resultant, in such an "unstressable" vector space one is justified in: (1) replacing the system of summing/multiplying translation vector components with a zero-vector, and (2) discarding the previous translation vector components of the zero-vector system. That is, one may properly equate the translation zero-vector system with a zero-vector, since the presence or absence of the combined vectors can have no further action. Specifically, axiomatically they exert no stress on the abstract vector space. Under those assumptions, the system can be replaced by its equivalent zero-factor alone.
Note that, applied to electromagnetics, this modeling procedure eliminates any theoretical possibility of electrogravitation (EM stress curvature of local space-time) a priori.
Force Vectors are Translations of Stress
Conceptually, a force vector is actually a release of some implied stress in a local medium. The force is applied to create stress in a second local region immediately adjacent to the primary region of stress. Of course the stress being thus "translated" by the force vector may be either tensile or compressive in nature, but a priori the force vector always represents the translation of that stress from its tail-end toward its head.
Consequently, an EM force vector is a gradient (inflow or outflow) in a scalar EM potential (stress), where the referent potential stress may be either tensile or compressive. Since modern Heaviside-type vectors do not distinguish between, or even recognize, the two "head and tail" scalar EM potentials involved in a vector, one needs to refer to Whittaker (36) to get it right. Whittaker, a fine mathematician in his own right, showed that any vector field can be replaced by two scalar waves. Unfortunately, the electrogravitational implications of Whittaker's profound work were not recognized and followed up, and their connection to Maxwell's quaternionic EM theory was not noticed nor examined.
So the idea of a vector EM force represents a release of a primary "tail-associated" scalar potential, and a bleedoff of that potential. It represents an increase in its primary "head-associated" scalar potential, and a bleed into that potential. Each scalar potential itself represents trapped EM energy density in the local vacuum, in the form of two or more (even an infinite number of) internal (infolded) EM force vector components (which may be either fixed, dynamic, or a blend of the two). The trapped energy density, however, may be either positive or negative with respect to the local energy density of the standard ambient vacuum, since the potential may be either compressive or tensile.
Maxwell's Electrogravitation Was Lost
Today we know that all potentials are gravitational and curve space-time; it is well-known in general relativity that gravitational curvature is simply the set of many potentials. One therefore can see that a vector EM wave represents a progressive translation wave in the vacuum EM potential - in the local EM-induced curvature of space-time. This EM change in local curvature of space-time moves away at the speed of light, producing only the most fleeting or momentary changes in curvature of any localized space-time region.
We note here as an aside: Only in a standing EM wave and in phase waves of coupled EM waves is there any deviation from the "momentary and then lost" change in the local space-time curvature. In those cases, the "persistence" of the local change in potential is an adverse function of frequency; hence at extremely low frequencies EM potential change persistence is sufficient to produce some very small electrogravitational effects. The effect is still slight, however, since the normal concept of "standing EM wave" represents a standing force vector situation, which is actually a stabilized spatial bleedoff of the potential. If a standing scalar EM wave is produced as in the two opposing pump waves in nonlinear optics pumped phase conjugate mirrors - then the stress is not primarily spatial, but temporal. Spatial effects then occur by particle-coupling - either in the virtual particle flux of vacuum or from the nucleus of an atom to the electron shells, and out into the material lattice structure. In the case of a standing scalar wave, electrogravitational effects are highly magnified because of the conversion of the primary potential stress to the time component. This increases the EG effects obtainable by a factor up to 9x10exp16. For this situation, at ELF standing scalar EM wave frequencies, very appreciable electrogravitational effects can be locally obtained.
The "Bottom Line" of EM Force-Field Theory
Thus concentrating only on the force fields of Maxwellian EM theory is equatable to concentrating on the situation where any localized electrogravitational effect that is temporarily formed is instantly released at the speed of light. The EG-effect in such a system is so small and fleeting, that the possibility of any persisting or significant local gravitational effects may be ignored.
Because of this, in any EM theory based only on the force fields and focusing only on their effects, then: (1) EM forces and their derivative effects may be represented by elementary Heaviside/Gibbs vector theory, including the equivalence of the zero-translation vector and any zero summed/multiplied system of nonzero translation vectors, (2) a system of EM forces which sum or multiply to a zero resultant may be discarded outright and the zero-vector substituted, (3) the effect of an EM potential is only to serve as an accumulator from which an EM force may be produced, and only its nonzero gradient will be thought to have any physical significance, (4) translation of EM forces (i.e., of potential gradients) and their effects on charged matter will assume primary importance, and (5) the potentials themselves may be regarded as simply mathematical conveniences and of little importance. This is precisely the subset of Maxwell's electromagnetics extracted and written so clearly by Heaviside.
As was Hertz, Heaviside was adamantly opposed to attaching any sort of physical reality to the potentials, preferring that they should be excised and "murdered". An indelible imprint - that potentials were "mysticism" and at best only mathematical conveniences - was imposed upon physics by Heaviside and Hertz (21). This rigid mindset was not to lessen (at least in quantum mechanics) until 1959; it was not to be assuaged until the mid-1960's (22) (37).
How EM Potentials are Regarded Today
So in 1988, we have finally arrived at the state where the potentials are more-or-less understood by a consensus of quantum physicists as being the primary EM reality, while the force fields are now seen to be secondary effects generated from the potentials.
This understanding, however, still has a long way to go before it penetrates the main bastions of physics and electrical engineering. Most scientists and electrical engineers are still adamantly committed to the Heaviside version of Maxwell's theory, and are strongly conditioned that the EM force fields are the primary effectors in electromagnetics.
They are also nearly totally resistant to the idea that there may be a fundamental error in automatically replacing a zero-resultant system of EM translation force vectors with a zero factor, rather than replacing the system with the combination of a conditional zero vector (conditional for translation only) and a scalar stress potential. Consequently, most orthodox scientists and engineers are still strongly conditioned against quaternions, and erroneously believe that Heaviside's translation was complete. Seemingly it has never occurred to most mathematicians and scientists that zero-vectors are usually not truly equal. Stress-wise, zero resultant combinant systems of multiple translation vectors usually differ in: (1) magnitude, (2) polarization, (3) type of stress, (4) frequency components, (5) nonlinear components, and (6) dynamic internal variation (38).
Vectors Versus Quaternions: The Cross Product
In a conventional 3-dimensional vector, one may have three vector components, such as (in Cartesian coordinates):
![]()
(1)
where
![]()
are unit vectors in the directions of the x, y and z axes respectively and a, b and c are constants. In the right side of equation (1), the three components of vector v are: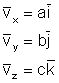
(2)
Obviously if the vector components of vector
![]()
are zero vectors, then:![]()
(3)
We shall be interested in the vector product of two identical vectors
![]()
, where![]()
x![]()
=![]()
(4)
where A is the length (magnitude) of vector
![]()
,![]()
is the angle between the two vectors (in this case zero), and![]()
is the zero vector.
After Heaviside and Gibbs, electrical engineers are trained to replace the cross product
![]()
x![]()
with the zero vector![]()
, discarding the components of the zero vector system as having no further consequences, either electromagnetically or physically.
Now let us look at the comparable quaternion expression of this situation. First, in addition to the three vector components, a quaternion also has a scalar component, w. So the quaternion q corresponding to vector
![]()
is:![]()
(5)
The physical interpretation of equation (5) is that there locally exists a stress w in the medium and a translation change
![]()
in that stress.
When the quaternion is multiplied times itself (that is, times an identical quaternion), the vector part zeros, just as it did for the vector expression. However, the scalar part does not go to zero. Instead, we have:
![]()
(6)
There is a very good physical interpretation of this result. The zero translation vector resultant
![]()
for the system shows that the system now does not produce translation of a charged particle. Because the force vectors have been infolded, the scalar term shows that the system is stressing, and the magnitude of that stress is given by the scalar term![]()
.
Notice that the zero vector in equation (6) does not represent the absence of translation vectors, but it represents the presence of a system of multiple (in this case, two) vectors, one of them acting upon the other in such a manner that their external translation effect has been lost and only their stress effect remains (39). The quaternion scalar expression has, in fact, captured the local stress due to the forces acting one on the other, so to speak. It is focused on the local stress, and the abstract vector space, adding a higher dimension to it.
In other words, the
![]()
in equation (6) represents the internal stress action of a nontranslating system of vectors that are present, infolded, and acting internally together on the common medium that entraps them and locks them together. The two translation vectors have formed a deterministically substructured medium-stressing system, and this is a local gravitational effect.
One sees that, if we would capture gravitation in a vector mathematics theory of EM, we must again restore the scalar term and convert the vector to a quaternion, so that one captures the quaternionically infolded stresses. These infolded stresses actually represent curvature effects in the abstract vector space itself. Changing to quaternions changes the abstract vector space, adding higher dimensions to it.
Artificial Electrogravitational Timestress
Let us assume for a moment that the two identical vectors
![]()
and![]()
are electric forces. Then![]()
represents the case where they are "locked together" in a local medium.
We now recall the modern quantum mechanical view that no "static" thing exists as such in the universe. A macroscopic "static" force - at quantum level - represents a continual constant rate of quantum change. In the case of an electrical force, it represents a continual constant rate of flux exchange of virtual photons.
The zero vector in equation (6) represents a constant exchange of macroscopically organized virtual energy into the local medium. Consequently, it represents continual internal work into and onto the local medium, but without translating it.
So a zero vector system of nonzero vector components represents internal or "infolded" constantly-working forces (internal to the medium) where the system does not cause translation of the point or region of application, whereas a nonzero vector and a nonzero vector system represent external forces which cause at least some translation of the point or region of application, unless this translation is nullified by other forces (40).
Physically, equation (6) may now be seen to state that: (1) internal forces (in the form of an internal stress) are present in the local medium but no translation force is present, and (2) these internal forces are continually performing internal work on the local medium without external translation. Since the translation vector component has spatially zeroed, then the scalar component that results may be taken to represent the time rate of expenditure of this internal work that is being done on the local medium - that is, it represents the extra internal power (which is simply the extra energy density of time) now being expended locally in and on the medium as a sink. If the vector components of the zero vector system are oriented outward, then the scalar stress component changes sign and it represents the extra internal power locally flowing out of the medium as a source.
Infolded Structuring is Dynamic and Complex
As can be realized, by changing the magnitudes, phasing, directions, rotations and dynamic frequencies of the vector components of the zero-vector stress system, very elaborate and sophisticated structuring of the local space-time medium (the local vacuum) may be deterministically constructed and controlled at will.
The continually performed internal work represents an increase or decrease in the local energy density of the medium, hence in the stress of the medium. However, note that this stress - either compressive or tensile is in and on the rate of flow of local time in the region. This timestress represents an artificial stress potential, where by "artificial" we mean that the timestress of the local medium is structured and macroscopically patterned (and controlled) deterministically; translation of that timestress is spatially radiating out over a finite macroscopic neighbourhood of the local point or region of application. This may be contrasted to a "natural" potential where the internal component stress vectors in the surrounding spatial neighbourhood are microscopic and randomly varying in all directions.
In equation (6), then, we have a local gravitational effect - a local increase in the energy density of a vacuum. Because the large EM force is utilized rather than the weak G-force, and because it is a timestress condition, it is a powerful local general relativistic effect. Because the local vacuum flux is significantly altered, we have a locally curved space-time which is significantly anisotropic, in violation to one of the fundamental (and crippling) assumptions of Einsteinian general relativity. Further, this is an electrogravitational effect. since it is a gravitational effect produced by purely electromagnetic means (41).
We have therefore produced a local curvature of space-time, and done so electromagnetically.
What is even more astonishing to the conventional relativist is that this local curvature startling enough in its own right - is also deterministically structured, and we can control the structuring at will. Hence we can engineer (structure) the vacuum itself (42).
But to return to equation (6).
The EG Sine-Squared Stress Wave
Suppose that
![]()
represents a time-varying![]()
-field vector and its amplitude is of the form:![]()
(7)
Then:
![]()
(8)
and this is a scalar EM stress wave, of variation of the local curvature of the vacuum. It is a powerful electrogravitational (scalar electromagnetic) wave, particularly if we produce it as a standing wave and use it to "pump" atomic nuclei in a rhythmically varying manner (43).
Briefly, a sine-squared wave has the appearance of a sort of "skinny" sine wave a near-sawtoothed wave that is now oscillating about an increased bias. In other words, the wave of equation (8) represents a scalar EM (an KG) wave that pumps the atomic nuclei of a targeted material, holding those nuclei at an excited average potential level. The wave has strong and very useful applications in - among other things - electrohealing. (44).
Example: Application to Explain Four-Wave Mixing
Now most modulations are represented by similar multiplication between two waves. Suppose we have two equal-amplitude, continuous monochromatic
![]()
-field sine-waves, introduced into a nonlinear dielectric medium in antiparallel and antiphased fashion (45). The medium will act as a modulator, causing the two waves to together", so that their![]()
-fields sum everywhere to a zero resultant vector spatially. A standing sine-squared scalar EM (electrogravitational) wave of the stress of time will be formed by the waves, very similar to equation (8) above.
This scalar wave will not appreciably react to the orbital electron shells of an atom of the dielectric, but will not pass through these outer "Faraday cages", reaching directly into the highly nonlinear nucleus itself.
We invoke the quantum mechanical picture of the nucleus as: (1) a region of local sharp curvature of space-time, (2) incredibly dynamic, with particles of every kind continually changing, transmuting, giving off other particles and waves, being absorbed, etc., (3) containing violent and dynamic charges and locally trapped fierce currents, and with field strength fluctuations reaching 10 and above, (4) in violent virtual particle exchange with the neighbouring vacuum, and (5) on the average, positively charged, so that it is -- on the average -- time reversed (46).
The presence of the sine-squared EG wave in the nucleus alters the nuclear potential by - on the average - the "DC" component potential amount. However, this delta in the potential is dynamic, varying as the sine-squared. This dynamically oscillating potential wave constitutes a pump wave on the nucleus itself, and it is rhythmically pumping the amplitude of the nuclear potential itself. We may think of the pumped nucleus as now conditioned to function as a parametric amplifier, ready to be given another "signal input" (47).
Now let us introduce yet another small sine wave into the nonlinear dielectric. It will modulate each of the two pump wave components, forming a scalar modulation upon the scalar sine-squared pump wave, and riding directly into the nucleus. In positive time, this now constitutes a "signal input" to the "parametric amplifier nucleus". The input is absorbed and amplified, up to the level of the pumping energy available in the pump wave that can be "scavenged up and gated".
Internal Absorption Can Be External Emission
However, the nucleus, being time reversed, also produces a time-reversed absorption which is seen spatially by the external observer as constituting emission! That is, in his own positive time, the external observer sees the time-reversed absorption as an emission event. Further, this is a time reversal - and hence an "emission" to the external observer of the entire parametrically amplified signal wave. (After all, in reversed time it is the pump wave that is modulating the signal wave - a principle of importance.)
So the powerfully amplified signal wave in the parametric amplifier is seen by the external spatial observer to be emitted from the nucleus. In short, a time-reversed and powerful scalar wave is emitted by the nucleus, passing back along the exact path taken by the original "signal wave". To a time-reversed entity, that invisible path is its path ahead of it in positive observer time. The external observer sees the emitted wave emerge as a powerfully amplified time-reversed EM wave, backtracking precisely back along the exact path taken by the signal wave, and appearing everywhere in phase spatially with the continuous signal wave.
In 4-space, of course, the time-reversed wave is out of phase in the fourth dimension, time.
Four-Wave Mixing is Like a Triode
This is the mechanism by which four-wave mixing provides a powerfully amplified time-reversed replica of the signal wave.
Note that the entire process can be compared to a triode: the signal wave constitutes the grid signal, the pump wave constitutes the plate voltage, and the nucleus of the atom in the dielectric provides the self-powered cathode.
We put in the signal wave (grid signal) and get out a 180-degree phase-shifted, amplified phase conjugate replica (amplified plate signal). The difference is that the PCR is phase-shifted in time, not space.
Negative Energy, Nuclear Binding and Transmutation
Note also that negative energy is already involved in the time-reversed nucleus of the atom, as in negative time (48). Excess "negative energy" in the nucleus means "additional binding energy", which will be expressed as additional inertia and coupled onto the electron shells. In this case the "inertial mass" of the pumped material increases, inversely as the pumping frequency. Less "negative energy" in the nucleus means "decreased binding energy", which places the nucleus in an unstable state. The nucleus can actually be transmuted by this means (in many cases toward barium, which apparently has the least binding energy per nucleon). Transmutation to an isomer appears easiest, though this is not always the case (49). It seems theoretically possible to design a complex pumping mixture of frequencies and power levels which will cause a specific radioactive nucleus to undergo transition to a harmless element or combination of elements. The main point is, scalar EM allows direct production of structured electrogravitational potentials in the nucleus, opening up the possibility of direct and controlled engineering of the nucleus itself.
Perspective
Obviously, in this short paper we have only scratched the surface. We have presented only the barest illustration of how Maxwell's original quaternion theory was actually a unified field theory of electrogravitation, where gravitation deals with the stress (enfolded and trapped forces) of the medium, and electrogravitation deals with the electromagnetic stress (enfolded and trapped EM forces) of the medium.
Of course, a great deal more work is necessary, but at least this indicates the way to go to obtain a unified field theory of electromagnetics and gravity that is practical and engineerable (50). I can only state that the indicated approach works in the laboratory, and let it go at that without further elaboration.
Recapitulation: From Maxwell to 1900
In summary, Maxwell himself was well-aware of the importance and reality of the potential stress of the medium (51). However, after Maxwell's death, Heaviside - together with Hertz - was responsible for striving to strip away the electromagnetic potentials from Maxwell's theory, and for strongly conditioning physicists and electrical engineers that the potentials were only mathematical conveniences and had no physical reality. Heaviside also discarded the scalar component of the quaternion, and - together with Gibbs - finalized the present modern vector analysis.
The scalar component of the quaternion, however, was the term which precisely captured the electrogravitational stress of the medium. By discarding this term, Heaviside (aided by Hertz and Gibbs) actually discarded electrogravitation, and the unified EM-G field aspects of Maxwell's theory. However, the theory and the calculations were greatly simplified in so doing, and this excision of electrogravitation provided a theory that was much more easily grasped and applied by scientists and engineers - even though they were now working in a subset of Maxwell's theory in which gravity and EM remained mutually exclusive and did not interact with each other.
Shortly before 1900, the vectorists' view prevailed, and the Heaviside version of Maxwell's theory became the established and universal "EM theory" taught in all major universities - and erroneously taught as "Maxwell's theory"! Though gravitation had been removed, the beautiful unification of the electrical and magnetic fields had been retained, and so the rise in applied and theoretical electromagnetics and electromagnetic devices began, ushering in the modern age.
Impact on Einstein's General Relativity Theory
Unfortunately, however, the excision of electrogravitation from Maxwell's theory was later to leave Albert Einstein with a quandary: it seemed that the only way space-time could be curved measureably was by and at a huge collection of mass, such as the Sun or a star. Accordingly, in constructing his theory of general relativity, Einstein assumed that the local space-time was never curved (since obviously the observer and his lab instruments would not be sitting on the surface of the Sun or of a distant star). Consequently, he did not write an unrestricted general theory of anisotropic space-time, but instead he wrote a highly restricted sort of "special relativity with distant perturbations" - which, nonetheless, was a revolutionary and epochal achievement.
Ironically, Einstein then spent the remainder of his life vainly trying to find a way to reintroduce electromagnetic fields into his general relativity, and to provide a unified field theory of gravity and electromagnetics. He failed, because his own prior assumption of a locally flat space-time had already effectively ruled out the very thing he sought.
Effect on Western Search For a Unified Field Theory
Today the magical unified theory of gravitation and electromagnetics continues to elude Western scientists, because they nearly universally adhere to Einstein's rejection of a locally-curved space-time. In so doing, the West largely rules out any local, laboratory-bench development of, and experimentation with, general relativistic systems. And in turn, that relegates general relativity to a non-experimental theory and, except for cosmological observations, a sort of "special relativity with distant perturbations."
The "locally flat space-time" assumption saves the conservation laws - and Western scientists have now become nearly totally dogmatic in their subservience to conservation. To challenge the conservation laws - and Einstein's restricted general relativity - leads to ostracization by his peers and vigourous suppression (52).
Soviet Theory of an Anisotropic Space-time
Soviet scientists, on the other hand, regularly publish papers where Einstein's crippling "local flat space-time" assumption is removed and the anisotropy of space-time is unrestricted, strongly implying that they might have developed an experimental unified field theory (53). They also are quite frank to publish statements that in a general relativistic system, conservation laws do not apply (54).
In numerous previous papers and books, the present authour has presented extensive evidence of the Soviet weaponization of electrogravitation and hence of a unified field theory (55).
Impact on Science and Humanity
Thus a great irony now is evident in Western science. More than 120 years ago, Maxwell wrote the first paper in his unified field theory of electrogravitation. Had Western scientists and mathematicians given greater attention to Maxwell's quaternion theory, by 1900 we should have been developing antigravity propulsion systems and interplanetary exploration vehicles.
Certainly humankind could have been lifted to much greater heights than where we are today. And along the way, we just might have avoided two great and bloody World Wars and a host of smaller ones.
In the modern geometrodynamic view, all forces are considered to arise from, and be rooted in, the curvature of space-time - in gravitation. If the curvature of space-time itself can easily be engineered and controlled by electromagnetic means, the extensive application of our present advanced state of electromagnetic development and devices can lead to control of the world of physical reality on a scale heretofore only dreamt of in the minds of our greatest visionaries.
Consider such a vision by Albert Einstein: Quoting:
"It would of course be a great step forward if we succeeded in combining the gravitational field and the electromagnetic field into a single structure. Only so could the era in theoretical physics inaugurated by Faraday and Clerk Maxwell be brought to a satisfactory close."
With the mastery of electrogravitation and the control of physical reality itself in our grasp, the freeing of humankind from want, misery, and poverty would directly follow. The impact on mankind's development would be almost beyond present human conception. Consider this vision from Teilhard de Chardin of the mastery of physical reality and the elimination of man's inhumanity to his fellow man:
"Someday, after we have mastered the winds, the waves, the tides and gravity, we shall harness for God the energies of love. Then for the second time in the history of the world man will have discovered fire."
Like Prometheus of old, in his quaternion EM theory James Clerk Maxwell produced a blazing coal of fire, literally taking the fire of gravitation from Olympus and giving it to human beings. Uncomprehending, scientists heaped ashes over the fiercely glowing coal, and only warmed themselves with the tiny trickle of electromagnetic heat that escaped the dampening ashes. For over a hundred years, the fiery coal has been quietly lying there, buried under the ashes, still glowing brightly.
It is time to be bold. For the enrichment of all mankind, let us uncover Maxwell's long-dormant fiery coal and fan into full bloom the Promethean flame of power that lies sleeping within.
Regards